前回の点、線分、ポリライン作成に続いて、今回は曲線を作成したいと思います。
通過点を指定して曲線を作る
曲線の場合、座標値の集合である線分やポリラインと違い曲線を定義する式を組み立て(ジオメトリーレベル)、そこからトポロジーレベルのシェイプを生成する必要があります。
コード
Standard_Integer nb_pts = 4; // 点数
// 点配列クラスに4点設定
Handle(TColgp_HArray1OfPnt) pary = new TColgp_HArray1OfPnt(0, nb_pts - 1);
pary->SetValue(0, gp_Pnt(0, 0, 0));
pary->SetValue(1, gp_Pnt(10, 0, 0));
pary->SetValue(2, gp_Pnt(10, 10, 0));
pary->SetValue(3, gp_Pnt(20, 20, 0));
Standard_Real tol = 1.0e-7; // トレランス(幾何誤差の許容値)
GeomAPI_Interpolate intp(pary, Standard_False, tol);
intp.Perform();
Handle(Geom_BSplineCurve) hgeom_bspc = intp.Curve();
TopoDS_Edge e = BRepBuilderAPI_MakeEdge(hgeom_bspc);
新しいクラスがいくつか出てきました。順を追って見てみましょう。
まず、Handle(TColgp_HArray1OfPnt) ですが、これは名前のとおり、gp_Pnt クラスの1次元配列コレクション TColgp_HArray1OfPnt の Handle 型です。 詳しい Handle の解説は別記事でしたいと思いますが、この型で定義されたオブジェクトは、new でインスタンスを作っても OCC 内に実装された独自のガベージコレクションが自動的に管理をしてくれるので、解放の必要がないオブジェクトになります。 使い方は普通のポインタ同様、アロー演算子でメソッドを呼び出します。
SetValue() でインデックスと点座標値を渡していきます。インデックスは1から開始されるので、注意してください。
次の GeomAPI_Interpolate は、通過点からBスプライン曲線を作成するためのクラスです。コンストラクタの第2引数を Standard_True にすると、曲線の始終点を曲線的に連結して輪状の曲線を作成します。
Perform() メソッドで計算を行い、Curve() メソッドで、ジオメトリーレベルの曲線シェイプ Geom_BSplineCurve の Handle 型を取得することができます。
さらに、BRepBuilderAPI_MakeEdge に渡すことにより、最終的に扱う TopoDS_Edge を受け取ることができます。
NURBS 曲線の要素から NURBS 曲線を作る
前提
このブログをご覧の方はご存じの方が大半だと思いますが、NURBS 曲線の定義は次の 3 つの要素から成ります。
- 次数
- 制御点列
- ノットベクトル列
制御点は x, y, z 座標値のほか、ウェイト w を持ちます。また、ノットベクトルの数は次の式により決定されます。
ノット数 = (制御点数) + (次数 + 1)
サンプル用の要素
- 次数: 2
- 制御点列: [100, 0, 0, 1], [70, -10, 10, 1], [30, 40, 10, 1.2], [0, 0, 0, 1]
- ノットベクトル列: [0, 0, 0, 1, 2, 2, 2]
これらの要素を用い、OCC 上のトポロジカルなシェイプを作成します。
コード
TColgp_Array1OfPnt poles(0, 3);
poles.SetValue(0, gp_Pnt(100, 0, 0));
poles.SetValue(1, gp_Pnt( 70,-10, 10));
poles.SetValue(2, gp_Pnt( 30, 40, 10));
poles.SetValue(3, gp_Pnt( 0, 0, 0));
TColStd_Array1OfReal weights(0, 3);
weights.SetValue(0, 1.0);
weights.SetValue(1, 1.0);
weights.SetValue(2, 1.2);
weights.SetValue(3, 1.0);
TColStd_Array1OfReal knots(0, 2);
knots.SetValue(0, 0.0);
knots.SetValue(1, 1.0);
knots.SetValue(2, 2.0);
TColStd_Array1OfInteger mults(0, 2);
mults.SetValue(0, 3);
mults.SetValue(1, 1);
mults.SetValue(2, 3);
Handle(Geom_BSplineCurve) hgeom_bscurve = new Geom_BSplineCurve(
poles, weights, knots, mults, 2, Standard_False);
TopoDS_Edge e = BRepBuilderAPI_MakeEdge(hgeom_bscurve);
上から、poles(制御点)、weights(制御点に対応するウエイト)、knots(ノットベクトル列)、mults(ノットベクトルの多重度)を設定し、Geom_BSplineCurve クラスのコンストラクタに渡しています。
ノットベクトルの多重度とはノットベクトルの各要素が「いくつ」続いているかを示すもので、この例では、
[0, 0, 0, 1, 2, 2, 2]
というノットベクトル列に対して、0 が 3 個、1 が 1 個、2 が 3 個と読み変え、
knots = [0, 1, 2]
mults = [3, 1, 3]
という引数を導き出すことができます。これは、例えば 0 が 100 個並ぶような巨大なノットベクトル列も
knots = [0]
mults = [100]
のように、シンプルに「圧縮」して表記できる利点があるためです。
この NURBS 曲線を表示してみると、次のようになりました。
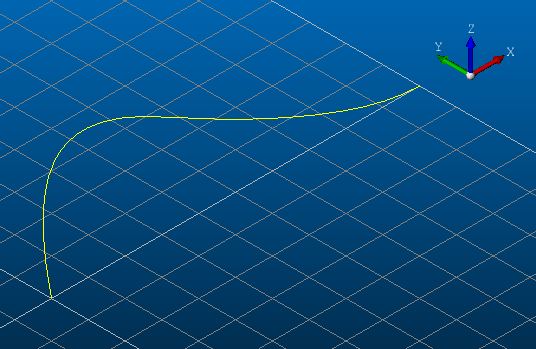
オマケ: ライブラリはどれ?
OCCには65個もの共有ライブラリが存在しており、自分が使いたいクラスがどのライブラリで定義されているのか、迷うことがあります。
OCCを使ったプログラミングで最低限必要なライブラリは、TKernel.so です。TKernel は間接的に tbb などのライブラリを参照しています。
さらに、自分が使いたいクラスのライブラリを調べるには、クラス・リファレンスの情報を参考にすればいいと思います。
例えば、BRepBuilderAPI_MakeEdge クラスを使いたい場合、クラス・リファレンスのページを参照すると、次のようになっていると思います。
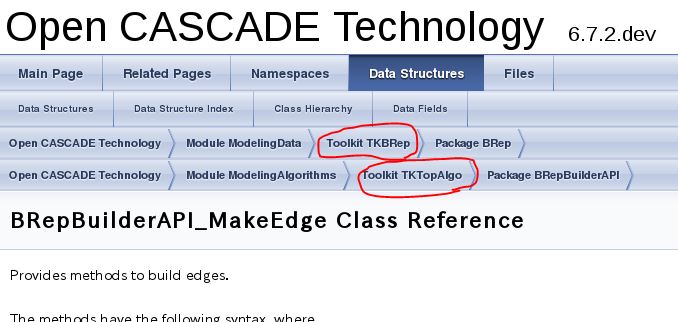
ここで、赤枠で示された Toolkit の名前がそのままライブラリ名になっています。この例では、BRepBuilderAPI_MakeEdge は TKBRep と TKTopAlgo が必要ということになります。
この情報を基に
g++ -lTKernel -lTKBRep -lTKTopAlgo -L/usr/lib/opencas -I/usr/include/opencascade source.cpp
という具合にリンクしてあげると良いと思います。
ちなみに Microsoft Windows のダイナミックリンクライブラリの場合も、同様に調べることができます。

[…] 前回の曲線に引き続き、今度は平面を作成していきたいと思います。 […]
[…] 前回の曲線に引き続き、今度は平面を作成していきたいと思います。 […]