小学生の頃に家族旅行でイギリスに行った時、母の友人がいるオックスフォード大学を訪ずれました。今でこそ世界有数の大学という事を知っていますが、子供だったので、広大な緑地帯で放し飼いされていたクジャクを追い回した記憶しかありません。
今日、仕事から帰ってきて夕食に一人鍋をしていると、テレビで「NHK オックスフォード白熱教室 第4回 数学が教える“知の限界”」が放送されていました。同大学マーカス・デュ・ソートイ教授によるカオス理論を中心にした、とっても分かりやすい内容の講義(もちろん、日本語吹き替え)で、いくつも興味深い内容のお話をやっていました。かなり一般的に楽しめる事を意識した講義だとは思いますが、難しい数式どころか、黒板すら使わずに話していて、数学が分からない自分にでも理解ができるものでした。残念ながら途中からしか見れなかったので、再放送などがあれば最初から見直してみたいと思います。
レミングの集団自殺
ある海外のドキュメンタリー番組で、レミングというネズミの一種が、4年に1度、崖から海へと一斉に飛び降りて自殺するという事が紹介されました。結局、後から番組関係者の証言によりヤラセであった事が分かったのですが、レミングの個体数が周期的に増減しているのは事実らしいです。
講義では、レミングの世代ごとの個体数をある式で表して、数学的な予測が可能な範囲と予測ができない範囲、つまりカオス状態に突入するところを分かりやすく説明しています。
ある世代の個体数を [math]N_{1}[/math] とした場合、次世代の個体数 [math]N_{2}[/math] は、次のように定義されるらしいです。
[math]N_{2} = ( N_{1} \cdot PN_{1} ) – \frac{ N_{1} \cdot PN_{1} }{T}[/math]
※ただし、[math]N_{2} \geqq 0[/math]
[math]\frac{ N_{1} \cdot PN_{1} }{T}[/math] の項が減少個体数を表し、[math]T[/math] の値が小さくなるにつれ総個体数は少なくなります。また [math]P[/math] は、ある世代と次世代に生まれた個体の総数の増加率を示す係数です。
[math]T[/math], [math]P[/math] をそれぞれ、[math]T = 10[/math], [math]P = 2[/math] とした場合、最初の世代 [math]N_{1}[/math] の値が [math]0 < N_{1} < T[/math] の時、世代を重ねるごとに収束して [math]N_{2} \fallingdotseq 5[/math] という結果に安定するらしいです。
分かりづらいので、最初の個体数が 2、 3、 8、 10 だった場合のグラフを書いてみました。
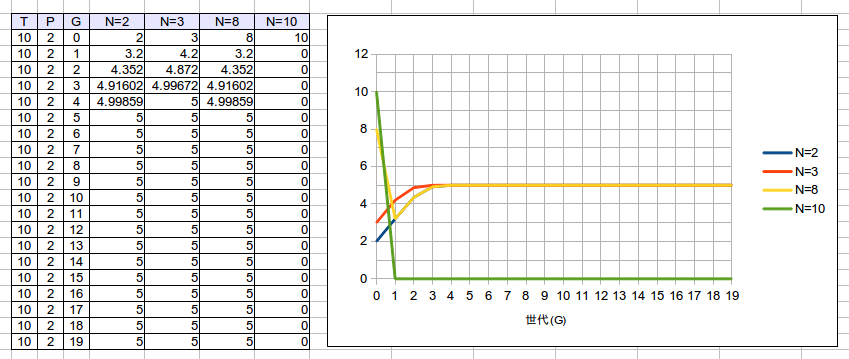
2、3、8 のいずれの場合も、最終的には 5 に収束して安定期に入ります。8 の場合、一度減った個体数が徐々に増えていくことが分かります。[math]T[/math] と同じ値の 10 は、増えることなく絶滅してしまいました。10 以上のどのような実数を与えても絶滅します。この式での最初の世代の上限は [math]N < T_{(10)}[/math] のようです。
次に、係数を [math]P = 2.5[/math] にして、最初の個体数を 2、3、9.9 だった場合のグラフを書きました。
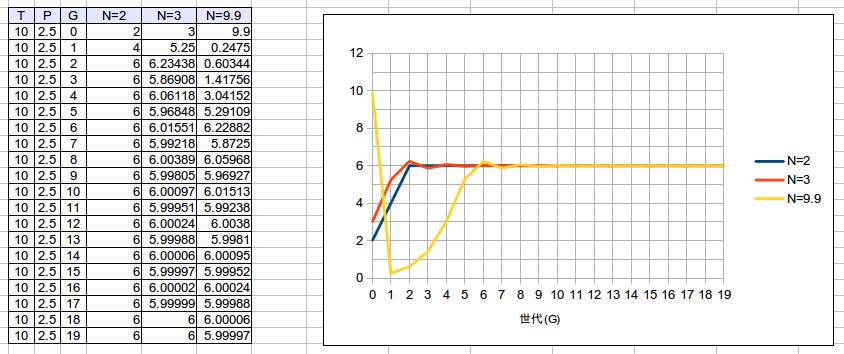
2 は 2 世代後には 6 に収束します。 3 は、6 の周辺に辿りついたあと増えたり減ったりしながら、やがて振れ幅が小さくなって 6 になります。9.9 の場合は、1 世代後に極端に値が減りますが、その後は徐々に回復していき、やがて 6 に収束しました。9.9 の場合の 1 世代後以降の折れ線は、[math]N = 0.1[/math] の時と同じものになります。同様に 9.5 の場合の 1 世代以降の折れ線は、0.5 の時と同じものになります。[math]T = N_{(9.5)} + N_{(0.5)}[/math] のようです。
さて、最終的に収束する値以上の値については、[math]T[/math] を超えない限り、1 世代以降でそれ以外の値と同じ折れ線になることが分かったので、2 と 3 の場合について、[math]P[/math] の値を変えて遊んでみましょう。
次のグラフは[math]P = 3[/math]の場合です。
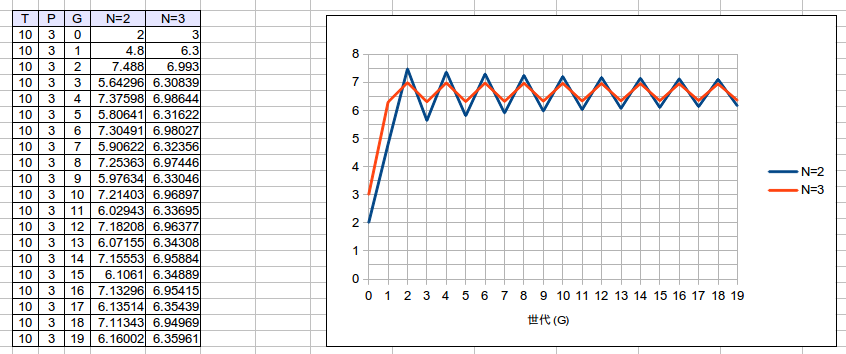
半ば予想どおりですが、今度は振れ幅がかなりゆっくりと小さくなっていっているようです。1 世代おきの増減が顕著に見ることができました。ここで、[math]P[/math] の値をどんどん上げることにより、振れ幅の衰退がどんどん小さくなっていき、限りなく周期的に増減をくりかえすグラフになるのかも!という期待が出てきます。
次に[math]P = 3.5[/math]の場合です。
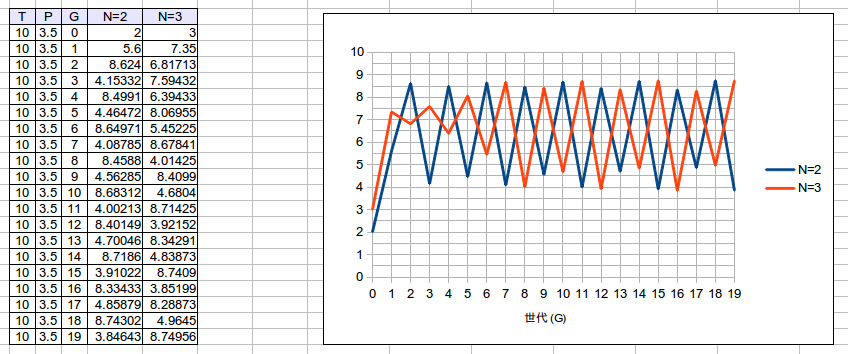
いきなり期待が裏切られました。3 の場合、最初の頃の振れ幅よりも途中から大きくなっています。
さらに[math]P = 3.7[/math]の場合、
かろうじて 1 世代おきに増減をくりかえしているものの、振れ幅の大きさがめちゃくちゃになりました。
そして[math]P = 4[/math]、
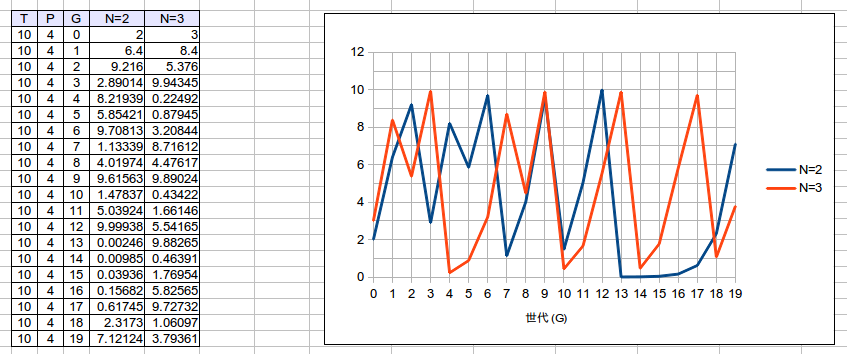
1 世代おきにくりかえしていた増減すらなくなり、完全に予測できないグラフとなりました。
番組では、4 年に一度、周期的に個体数を極端に減らすレミング題材にして、このようなグラフを紹介していました。[math]P[/math] と最初の個体数によって、レミングの個体数に似たグラフを表現できるということです。さらに、上で試してみたとおり、この式では [math]P[/math] が 3.5 から周期性が失なわれ始め、4 になると予測不可能なめちゃくちゃな状態、つまり「カオス状態」に突入することも紹介していました。
このレミングの話の前に、重力がお互いに影響し合う惑星の軌道や、複数の磁石を用いた振り子、二重振り子の話がありました。そこで、ささいな初期状態の変化が結果的には、予測不可能なカオス状態へ突入しかねないバタフライ効果についても触れていました。
余談ですが、番組では 4 までしか触れていなかったので、「[math]P[/math] の値を上げれば上げるほど、折れ線はどんどんカオス状態になっていくんだろうなあ」という淡い期待をしてしまいましたが、実際には…
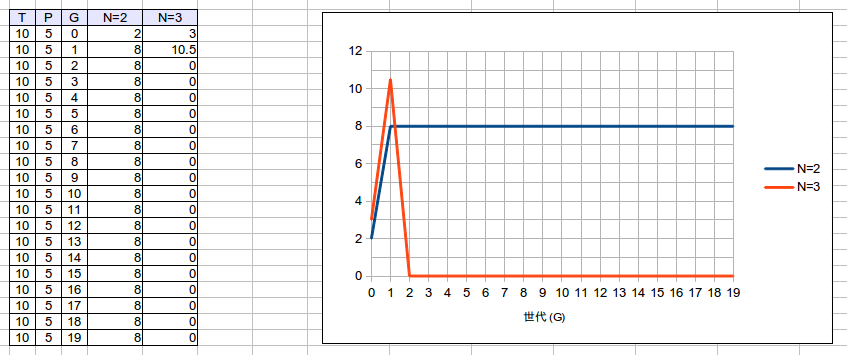
[math]P = 5[/math]の場合、2 が 8 に収束するわ、3 が [math]T[/math] を超えていないにも関わらず、絶滅してしまうわ、グラフの折れ線的にはグラフの後の世代を予測できる非カオス状態になりましたが、これまでの考え自体を否定する結果となりました。
そもそも、そういう挙動をする式だと言ってしまえばそれまでですが、初期状態の小さな変化によって、結果が予測不可能なものになる分かりやすい例えだったと思います。